class="empty-line"/>
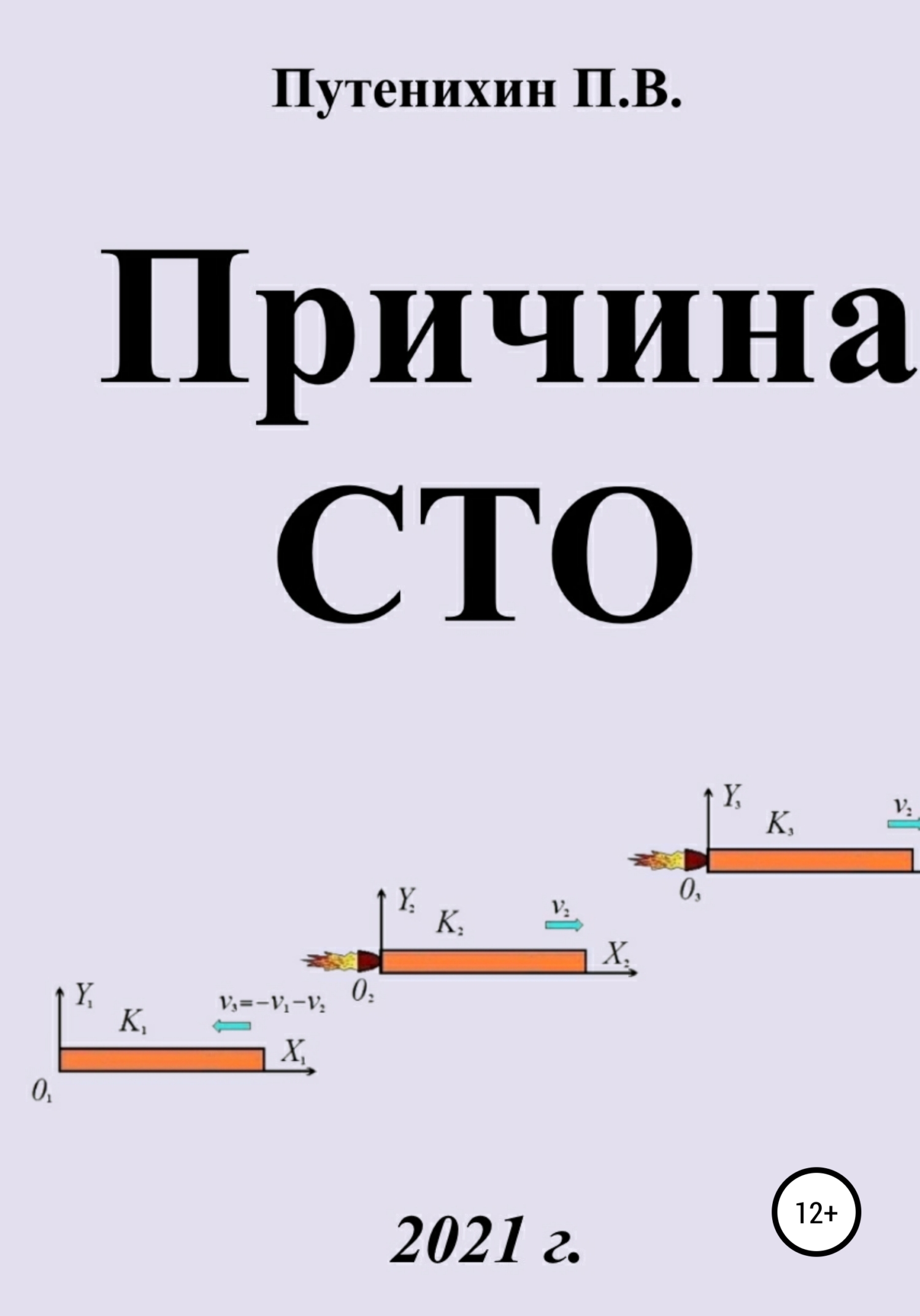
Для определения введённых параметров γ и σ, исходя из принципа относительности (первый постулат СТО) — равноправия всех инерциальных систем отсчета, рассмотрим три такие произвольные ИСО — K1, K2 и K3.
Установим, что система K2 движется относительно K1 со скоростью v1, система K3 — относительно K2 со скоростью v2 и система K1 — относительно K3 со скоростью v3=-(v1+ v2):
Рис. 4 Три системы отсчета, движущиеся друг относительно друга.
Пометим координату x и время t цифровыми индексами, соответствующими номерам систем, к которым они относятся, и запишем преобразования для каждой из них:
Подставим x3 и t3 из второй системы уравнений в третью:
Раскроем круглые скобки:
Вынесем за скобки общие множители:
и сгруппируем общие члены:
Полученные уравнения должны иметь (и имеют) такой же вид, что и уравнения системы (9). Это значит, что, как и в системе уравнений (9) в этой системе коэффициенты при первых слагаемых в уравнениях — один и тот же коэффициент:
После сокращения и элементарных преобразований получаем:
Из этого равенства следует, что следующие отношения имеют одно и то же значение для всех систем отсчёта, независимо от скорости их движения:
Это отношение мы обозначили квадратом величины (константы) "c" — по первой букве слова "const". Поясним, почему необходимо приравнять отношения именно квадрату. Из второго уравнения системы (9) следует, что все полученные отношения имеют размерность квадрата скорости. Чтобы убедиться в этом, анализируем размерности величин (индекс "разм" означает, что рассматривается не значение, а размерность величин):
Очевидно, что в скобках стоят величины с размерностью времени. Отсюда следует, что квадрат размерности константы "c" равен квадрату размерности скорости, а сама величина "с" имеет, соответственно, размерность скорости:
Это и означает, что все отношения (10) равны квадрату некоторой величины "с".
Уравнения (9) должны быть справедливы и для обратного преобразования, когда системы отсчёта "меняются местами". Относительная скорость при этом меняет свой знак:
Подставим в это уравнение значения штрихованных величин из исходной системы (9):
и окончательно:
Из соотношений (10) находим:
Подставляем это значение в (11) и получаем:
В результате преобразований получаем:
Функция γ(v) является четной. Это видно из следующих соображений. Если мы развернём оси двух систем отсчёта на 180о, то скорость также изменит свой знак. Это равнозначно тому, как если бы мы смотрели на эти системы через зеркало (зеркало заднего вида автомобиля): направления осей и движения развернутся. Следовательно, первое уравнение системы (9) будет иметь вид:
Сравнивая эти уравнение, получаем:
Раскрываем скобки:
и получаем признак четности функции:
Подставляем полученное значение (13) в (12) и находим:
Теперь находим значение функции гамма:
и подставляем его в уравнения (9):
Имея два этих уравнения, можно легко вывести все остальные следствия преобразований Лоренца, как это было показано в предыдущем разделе.
Итак, мы вывели явный вид уравнений (6) преобразования между двумя инерциальными системами отсчёта и получили уравнения Лоренца (14), в которые мы были вынуждены ввести некую константу с, значение которой нам, строго говоря, неизвестно. Дотошный читатель, наверное, уже давно держит в голове мысль: когда же, наконец, и каким образом автор статьи объявит эту константу скоростью света. По мнению ряда авторов, вопрос этот не простой. Например, С.Степанов считает (у него эта константа α является обратной величиной к нашей константе — с), что "функциональная форма преобразования между наблюдателями двух инерциальных систем отсчёта полностью определяется с точностью до константы α. Выяснение её значения и знака — это уже вопрос экспериментальный. Фундаментальная константа α могла оказаться и нулевой, однако в нашем Мире она больше нуля" [2].
На сайте библиотеки Физического факультета СПбГУ С.Н.Манида (у него величина g также является обратной величиной к нашей константе с): "вводит некоторую постоянную величину, размерность которой — обратный квадрат скорости. Эта величина одинакова во всех системах отсчета, и ее численное значение не может быть выведено из каких-либо общих принципов. Экспериментальное значение этой величины g=c-2, где c — скорость света в вакууме" [1].
"мы вывели соотношения из принципа относительности и получили следствием постоянство скорости c во всех инерциальных системах отсчета. Важно отметить принципиальное отличие данного подхода к выводу преобразований Лоренца от общепринятого. Постоянство скорости света во всех инерциальных системах отсчета — это экспериментальный факт, установленный с определенной степенью точности. Приведенный выше вывод не опирается на этот факт, из него следует только существование скорости, одинаковой во всех инерциальных системах отсчета" [1].
На одном из форумов в интернете опубликован анализ статьи Фейгенбаума, посвященной, в частности, выводу соотношений СТО из принципа относительности. Там сказано:
"Чтобы вывести "специальную теорию относительности" (СТО) постулат постоянства скорости света не нужен.
Это значит, что возможно, что скорость света не постоянна (если она меньше фундаментальной константы C). Формулы СТО — логически не зависят от постулата постоянства скорости света. Фейгенбаум пишет, что СТО можно было бы открыть ещё во времена Галилея. Всё, что для этого нужно, это — принцип равноправности равномерно движущихся относительно друг друга систем (принцип относительности Галилея) и изотропия пространства" [3].
Проводится анализ самой константы, аналога скорости света:
"Ясно только, что подход Фейгенбаума кардинально меняет всё наше понимание того, что такое